FUNCIONES
MATEMATICAS COMUNES
Funciones
trigonométricas
MATLAB opera con los ángulos en radianes
siempre.Puedes intentar hacer lo siguiente:
-
Calcular el seno de un ángulo recto
-
Calcular el seno de 45º
-
Calcular el arcotangente de 1
Números
Complejos
-
Resolver una ecuación de segundo grado
ax2+bx+c=0 con los valores siguientes:
-
a = 1 , b=5 , c=6
EDU»
a=1;b=5;c=6;
EDU»
x1=(-b+sqrt(b^2-4*a*c))/(2*a)
x1
=
-2
EDU»
x2=(-b-sqrt(b^2-4*a*c))/(2*a)
x2
=
-3 |
-
Sustituir las dos raíces para comprobar
la respuesta.
-
Recalcular con a=1, b=4, c=13
-
Introducir los números complejos siguientes
 c1 = 1- 2i c1 = 1- 2j
c1 = 1- 2i c1 = 1- 2j
-
Cambio de la forma polar a rectangular. Uso
de real, imag, abs y angle.
real(x) devuelve la parte real
del número complejo x
imag(x) devuelve la parte imaginaria
del número complejo x
abs(x) devuelve el valor absoluto
del número complejo x
angle(x) devuelve el ángulo
de un número complejo
EJERCICIOS:
2.1)Expresa en forma
polar el número complejo: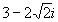 .SOLUCIÓN .SOLUCIÓN
2.2) Sean z1=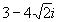 y z2=-7i 16, calcular la parte real e imaginaria de z1*z2 y
de z1+z2.SOLUCIÓN
y z2=-7i 16, calcular la parte real e imaginaria de z1*z2 y
de z1+z2.SOLUCIÓN
2.3) Calcular
2.3.1) (4-3i)+(2i-8)
2.3.2) 3(-1+4i)-2(7-i)
2.3.3) (3+2i)(2-i)
2.3.4) (i-2)(2(1+i)-3(i-1)
2.3.5) (2-3i) /
(4-i)
2.3.6) (2+i)(3-2i)(1+2i)
/ (1-i)2
2.3.7) (i4
+ i9 + i16) / (2 - i5 - i10
- i15)
SOLUCIÓN
2.4) Sean z1
= 1- i , z2 = -2 + 4i y 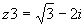 .Calcular .Calcular
2.4.1) (z1)2 + 2(z1) - 3
2.4.2)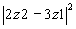
2.4.3) Re (2z13 + 3z22 – 5z32)
2.4.4) Im (z1z2/z3)
SOLUCIÓN
2.5) Expresar los
siguientes números complejos en forma polar:
2.5.1) 2-2i
2.5.2)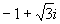
2.5.3) - i
2.5.4) - 4
2.5.5)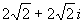
2.5.6)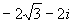
2.5.7) - 3 - 4i
2.5.8) 1 – 2i
Representar vectorialmente
los 8 números complejos anteriores.
SOLUCIÓN |