|
SOLUCIONES A LOS EJERCICIOS
Tema 1
1.1)
EDU»
pera=3.25
pera
=
3.2500
EDU»
Pera=5;
EDU»
perA=6/7
perA
=
0.8571
EDU»
PERA=3*pera
PERA
=
9.7500
EDU»
PERA % rational
PERA
=
39/4
EDU»
PERA % long
PERA
=
9.75000000000000
EDU»
who
Your
variables are:
PERA
Pera perA pera
EDU»
clear pera
EDU»
who
Your
variables are:
PERA
Pera perA
EDU»
save ejemploa
EDU»
load ejemploa
EDU»
who
Your
variables are:
PERA
Pera perA |
Tema 2
2.1)
EDU»
c=3-2*sqrt(2)*i
c =
3.0000
- 2.8284i
EDU»
angle(c)
ans
=
-0.7560
EDU»
abs(c)
ans
=
4.1231
El número
complejo sería 4.1231-0.7560 |
2.2)
EDU»
z1=3-4*sqrt(2)*i
z1 =
3.0000
- 5.6569i
EDU»
z2=-7*i^16
z2 =
-7.0000
+ 0.0000i
EDU»
w=z1*z2
w =
-21.0000
+39.5980i
EDU»
real(w)
ans
=
-21.0000
EDU»
imag(w)
ans
=
39.5980
EDU»
v=z1+z2
v =
-4.0000
- 5.6569i
EDU»
real(v)
ans
=
-4
EDU»
imag(v)
ans
=
-5.6569 |
Tema 3
3.1)
EDU»
a=[1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20];
EDU»
a(7:3:20)
ans
=
7 10
13 16 19
EDU»
a(20:-3:7)
ans
=
20 17
14 11 8 |
3.2)
EDU»
a=[2 -3 7];
EDU»
b=[4 0 -1];
EDU»
a./2
ans
=
1.0000
-1.5000 3.5000
EDU»
2*a
ans
=
4 -6
14
EDU»
dot(a,b)
ans
=
1 |
Tema 4
4.1)
| EDU»
x=[0:pi/8:pi/2];
EDU»
y=cos(x);
EDU»
plot(x,y)
EDU»
xlabel('variable x')
EDU»
ylabel('cos(x)')
EDU»
title('mi primer dibujo') |
Ver dibujo |
EDU»
x=linspace(0,pi/2,20)
x =
Columns
1 through 7
0 0.0827
0.1653 0.2480 0.3307 0.4134 0.4960
Columns
8 through 14
0.5787
0.6614 0.7441 0.8267 0.9094 0.9921 1.0748
Columns
15 through 20
1.1574
1.2401 1.3228 1.4054 1.4881 1.5708
EDU»
y=cos(x);
EDU»
plot(x,y,'+') |
Ver dibujo |
4.2)
EDU»
x=[-1:0.2:2.8]
x =
Columns
1 through 7
-1.0000
-0.8000 -0.6000 -0.4000 -0.2000 0 0.2000
Columns
8 through 14
0.4000
0.6000 0.8000 1.0000 1.2000 1.4000 1.6000
Columns
15 through 20
1.8000
2.0000 2.2000 2.4000 2.6000 2.8000
EDU»
y=x.^2-5*x+8;
EDU»
plot(x,y)
EDU»
grid
EDU»
hold on
EDU»
y=x.^3+1;
EDU»
plot(x,y,’+’) |
Ver dibujo |
Tema 5
5.1)
EDU»
x=3;
EDU»
if x>2
y=x^3-5
else
y=3
end
y =
22 |
5.2)
EDU»
compra=3500;
EDU»
if 0<compra<5000
factura=(1-3/100)*compra
elseif
5000<compra<10000
factura=(1-5/100)*compra
elseif
compra>10000
factura=(1-10/100)*compra
end
factura
=
3395 |
Tema 6
6.1)
Creamos
un fichero .M
New--M-file
if 0<compra<5000
factura=(1-3/100)*compra
elseif
5000<compra<10000
factura=(1-5/100)*compra
elseif
compra>10000
factura=(1-10/100)*compra
end |
Guardar como factura.m
Nos vamos a la pantalla inicial :
EDU»
compra =6000;
EDU»
factura
factura
=
5820
EDU»
compra=11000;
EDU»
clear factura
EDU»
factura
factura
=
10670 |
Tema 9
9.1)
EDU»
A=[3 7 -3
0 9
1
-4 6
0]
A =
3 7
-3
0 9
1
-4 6
0
EDU»
A'
ans
=
3 0
-4
7 9
6
-3 1
0
EDU»
inv(A)
ans
=
0.0390
0.1169 -0.2208
0.0260
0.0779 0.0195
-0.2338
0.2987 -0.1753
EDU»
det(A)
ans
=
-154 |
9.2)
EDU»
A=[1 -1 1
3 2
-2
-1 3
-1];
EDU»
b=[2 1 2]'
b =
2
1
2
EDU»
x=inv(A)*b
x =
1.0000
2.0000
3.0000 |
9.3)
EDU»
A=[1 1 1 1
1 -1
2 1
2 0
1 1
4 2
-1 2];
EDU»
for j=2:5
A(j-1,:)=A(j-1,:)/A(j-1,j-1);
for
i=j:4
A(i,:)=A(i,:)-A(j-1,:)*A(i,j-1);
end;
end;
EDU»
A
A =
1.0000
1.0000 1.0000 1.0000
0 1.0000
-0.5000 0
0 0
1.0000 0.5000
0 0
0 1.0000 |
9.4)
EDU»
A=[1 1 1 1 10
1 -1
2 1 9
2 0
1 1 9
4 2
-1 2 13]
A =
1 1
1 1 10
1 -1
2 1 9
2 0
1 1 9
4 2
-1 2 13
EDU»
rref(A)
ans
=
1 0
0 0 1
0 1
0 0 2
0 0
1 0 3
0 0
0 1 4 |
Por lo tanto, las soluciones son x=1, y=2, z=3 y w=4.
9.5)
EDU»
A=[1 1 1 1
1 1
-1 -1
1 -1
1 -1
1 -1
-1 1];
EDU»
[v,d]=eig(A) % v es la matriz de paso y d es la matriz de jordan
v =
0.8336
0.0533 0.2285 -0.5000
0.4434
-0.6434 -0.3734 0.5000
0.3223
0.7610 -0.2590 0.5000
0.0680
-0.0643 0.8610 0.5000
d =
2.0000
0 0 0
0 2.0000
0 0
0 0
2.0000 0
0 0
0 -2.0000
EDU»
A^2 % observar que A2 es lo mismo que d2(y sin embargo
la operación d2, es mucho más sencilla)
ans
=
4 0
0 0
0 4
0 0
0 0
4 0
0 0
0 4
EDU»
d^2
ans
=
4.0000
0 0 0
0 4.0000
0 0
0 0
4.0000 0
0 0
0 4.0000
EDU»
inv(A)
ans
=
0.2500
0.2500 0.2500 0.2500
0.2500
0.2500 -0.2500 -0.2500
0.2500
-0.2500 0.2500 -0.2500
0.2500
-0.2500 -0.2500 0.2500
Otra
forma
EDU»
[v,j]=jordan(A)
v =
[ 1/4,
3/4, 1, 1]
[-1/4,
1/4, 0, 0]
[-1/4,
1/4, 1, 0]
[-1/4,
1/4, 0, 1]
j =
[-2,
0, 0, 0]
[ 0,
2, 0, 0]
[ 0,
0, 2, 0]
[ 0,
0, 0, 2] |
9.6)
EDU»
A=[2 5 7
-1 2
0
1 6
1]
A =
2 5
7
-1 2
0
1 6
1
EDU»
expm(A)
ans
=
-23.7331
41.6026 -18.0871
1.4238
-31.8534 -8.1203
-9.5441
-9.7031 -15.3491 |
9.7)
EDU»
A=[3 -1 2;1 2 3;2 -2 -1];
EDU»
[L,U]=lu(A)
L =
1.0000
0 0
0.3333
1.0000 0
0.6667
-0.5714 1.0000
U =
3.0000
-1.0000 2.0000
0 2.3333
2.3333
0 0
-1.0000 |
TEMA 10
10.1)La función:
function
y=f(x)
%calcula
el valor de f en un punto
if x>2
f(x)=3*x-5;
else
f(x)=4*x-1;
end;
f(x)
Calculo
f(2):
EDU»
x=2;
EDU»
f(x)
ans
=
7 |
TEMA 11
11.1)
EDU»
p=[1 0 -3 0 7];
EDU»
roots(p)
ans
=
-1.4397
+ 0.7569i
-1.4397
- 0.7569i
1.4397
+ 0.7569i
1.4397
- 0.7569i |
REPASO GENERAL
a)
EDU» A=[1 6 4;3 -1 0;5 2 -5];B=[1 5 -1;3
4 7;2 -2 -6];
EDU» A+B
ans =
2 11 3
6 3 7
7 0 -11
EDU» A-B
ans =
0 1 5
0 -5 -7
3 4 1
EDU» A*B
ans =
27 21 17
0 11 -10
1 43 39
EDU» inv(A)
ans =
0.0360 0.2734 0.0288
0.1079 -0.1799 0.0863
0.0791 0.2014 -0.1367
b) EDU» A=[3 2 -4;4 3
-7;-1 6 5];
EDU» b=[2 -1 4];
EDU» x=inv(A)*b'
x =
3.7838
-0.4595
2.1081
c)La función .m es
function [potencia5]=pot5(x)
%calcula la potencia quinta de x
potencia5=x^5;
disp('la potencia quinta de ')
x
disp('es')
potencia5;
Llamando:
EDU» pot5(2)
la potencia quinta de
x =
2
es
ans =
32
d)La función .m es:
function [media,estad]=estad(x)
%estad devuelve dos valores ,uno la media
%y otro la desviación del vector x
[m,n]=size(x);
media =sum(x)/m
desv=sqrt(sum(x.^2)/m-media.^2)
Llamando:
EDU» x=[13 46 82 10];
EDU» estad(x)
media =
151
desv =
0+ 1.1701e+002i
ans =
151
e) EDU» t=[-pi:pi/16:pi];
EDU» y=cos(3*t);z=sin(2*t);
EDU» plot(y)
EDU» hold on
EDU» plot(z)
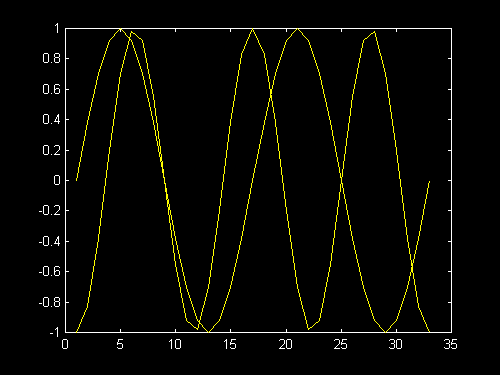
|