|
MATRICES.Resolución
de sistemas
Resolución
de sistemas de ecuaciones algebraicas lineales
Ejemplo:
Dado
el sistema de ecuaciones algebraicas lineales siguiente:
1x1+2x2+3x3
=
366
4x1+5x2+6x3
=
804
7x1+8x2+9x3
=
351
se
puede expresar matricialmente de la forma siguiente:
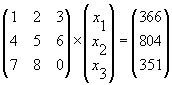
A X = b
Premultiplicando por la inversa de A, A-1
obtenemos:
X = A-1 b
Siguiendo
con el ejemplo anterior:
EDU»
A=[1 2 3
4
5 6
7
8 0];
EDU»
b=[366 804 351]';
EDU»
x=inv(A)*b
EDU»
x % Son las soluciones del sistema de ecuaciones anterior.
x
=
25
22
99 |
Observar que b debe ir traspuesta, ya
que si no, por defecto, b es un vector fila y no se podría realizar
el producto.
Reducción
del tamaño de una matriz
Para reducir el tamaño de la matriz
B anterior eliminando la última columna se usa [ ] (2 corchetes)
Ejemplo:
EDU»
B(:,3)=[] % le estamos indicando que borre la tercera columna
B
=
1
3
3
4
1
3 |
Reducción
a la forma escalonada por filas. Reducción de Gauss
Ejemplo:triangularizar
una matriz. Sea la matriz A siguiente:
-4
3 2 5
-2
1 -1 2
-4
1 1 4
3
-6 -4 -5
triangularizarla
mediante el método de Gauss. Obtener la forma escalonada por filas.
EDU»
A=[ -4 3 2 5
-2
1 -1 2
-4
1 1 4
3
-6 -4 -5]
A
=
-4
3 2 5
-2
1 -1 2
-4
1 1 4
3
-6 -4 -5
EDU»
A(1,:)=A(1,:)/A(1,1) % dividimos la primera fila por -4
A
=
1.0000
-0.7500 -0.5000 -1.2500
-2.0000
1.0000 -1.0000 2.0000
-4.0000
1.0000 1.0000 4.0000
3.0000
-6.0000 -4.0000 -5.0000
EDU»
for i=2:4
A(i,:)=A(i,:)-A(1,:)*A(i,1)
end; |
Con
el bucle for, hacemos ceros en la primera columna.
EDU»
A
A
=
1.0000
-0.7500 -0.5000 -1.2500
0
-0.5000 -2.0000 -0.5000
0
-2.0000 -1.0000 -1.0000
0
-3.7500 -2.5000 -1.2500
EDU»
A(2,:)=A(2,:)/A(2,2) % dividimos la segunda fila por –0.5
A
=
1.0000
-0.7500 -0.5000 -1.2500
0
1.0000 4.0000 1.0000
0
-2.0000 -1.0000 -1.0000
0
-3.7500 -2.5000 -1.2500 |
Seguimos
con el mismo esquema.
Hacemos
ceros en la segunda columna con el bucle for
for
i=3:4
A(i,:)=A(i,:)-A(2,:)*A(i,2)
end;
A
=
1
-0.75 -0.5 -1.25
0
1 4 1
0
0 7 1
0
0 12.5 2.5 |
Dividimos
la tercera fila por 7
A(3,:)=A(3,:)/A(3,3)
A=
1
-0.75 -0.5 -1.25
0
1 4 1
0
0 1 0.1429
0
0 12.5 2.5 |
Hacemos
ceros en la tercera columna
for
i=4:4
A(i,:)=A(i,:)-A(3,:)*A(i,3)
end;
A
=
1
-0.75 -0.5 -1.25
0
1 4 1
0
0 1 0.1429
0
0 0 0.7143 |
Dividimos
la cuarta fila por 0.7143
A(4,:)=A(4,:)/A(4,4)
A
=
1
-0.75 -0.5 -1.25
0
1 4 1
0
0 1 0.1429
0
0 0 1 |
El programa completo que triangularizará
una matriz nxn será:
for j=2:n+1
A(j-1,:)=A(j-1,:)/A(j-1,j-1);
for i=j:n
A(i,:)=A(i,:)-A(j-1,:)*A(i,j-1);
end;
end;
Ejemplo:
EDU»
for j=2:n+1
A(j-1,:)=A(j-1,:)/A(j-1,j-1);
for
i=j:n
A(i,:)=A(i,:)-A(j-1,:)*A(i,j-1);
end;
end;
EDU»
A
A
=
1.0000
-0.7500 -0.5000 -1.2500
0
1.0000 4.0000 1.0000
0
0 1.0000 0.1429
0
0 0 1.0000 |
Forma
escalonada reducida por filas de una matriz. Método de Gauss-Jordan.
Función RREF.
La función rref calcula la forma
escalonada reducida por filas de una matriz que brinda en este caso de
forma cómoda la solución del sistema de ecuaciones anterior.
En el sistema de ecuaciones anterior la
matriz ampliada es:
Ejemplo:
A
=
1
2 3 366
4
5 6 804
7
8 0 351
EDU»
rref(A)
ans
=
1
0 0 25
0
1 0 22
0
0 1 99 |
Una aplicación : Distribución
de calor.
Se tiene una placa rectangular cuyas orillas
se mantienen a cierta temperatura. Se tiene interés en encontrar
la temperatura en los puntos interiores conocida la de algunos puntos en
el borde. Considerar el siguiente diagrama. Se quiere encontrar una aproximación
de las temperaturas en los puntos intermedios T1 a T9, suponiendo que la
temperatura en un punto interior es el promedio de la de los cuatro puntos
que la rodean.
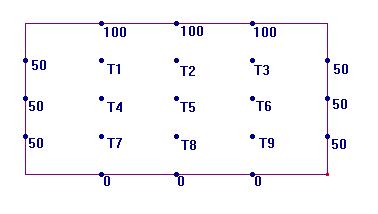
Divididas todas las ecuaciones por 4
T1 = 150 + T2 + T4
T2 = 100 + T1 + T3 + T5
T3 = 150 + T2 + T6
T4 = 50 + T1 + T5 + T7
T5 = T2 + T4 + T6 + T8
T6 = 50 + T3 + T5 + T9
T7 = 50 + T4 + T8
T8 = 0 + T5 + T7 + T9
T9 = 50 + T6 + T8
Matriz de coeficientes:
t =
-4 1 0 1 0 0 0 0 0
1 -4 1 0 1 0 0 0 0
0 1 -4 0 0 1 0 0 0
1 0 0 -4 1 0 1 0 0
0 1 0 1 -4 1 0 1 0
0 0 1 0 1 -4 0 0 1
0 0 0 1 0 0 -4 1 0
0 0 0 0 1 0 1 -4 1
0 0 0 0 0 1 0 1 -4
Matriz de términos independientes
EDU»
ind=[150 100 150 50 0 50 50 0 50]
ind
= 150 100 150 50 0 50 50 0 50
EDU»
ind=-ind
ind
= -150 -100 -150 -50 0 -50 -50 0 -50
Soluciones
EDU»
x=inv(t)*ind'
x
=
475/7
500/7
475/7
50
50
50
225/7
200/7
225/7
EDU»
format
EDU»
x
x
=
67.8571
71.4286
67.8571
50.0000
50.0000
50.0000
32.1429
28.5714
32.1429 |
Otra solución hubiera sido utilizar
rref
ampliada=[t,ind']
ampliada
=
-4
1 0 1 0 0 0 0 0 -150
1
-4 1 0 1 0 0 0 0 -100
0
1 -4 0 0 1 0 0 0 -150
1
0 0 -4 1 0 1 0 0 -50
0
1 0 1 -4 1 0 1 0 0
0
0 1 0 1 -4 0 0 1 -50
0
0 0 1 0 0 -4 1 0 -50
0
0 0 0 1 0 1 -4 1 0
0
0 0 0 0 1 0 1 -4 -50
EDU»
rref(ampliada)
ans
=
1
0 0 0 0 0 0 0 0 67.8571
0
1 0 0 0 0 0 0 0 71.4286
0
0 1 0 0 0 0 0 0 67.8571
0
0 0 1 0 0 0 0 0 50.0000
0
0 0 0 1 0 0 0 0 50.0000
0
0 0 0 0 1 0 0 0 50.0000
0
0 0 0 0 0 1 0 0 32.1429
0
0 0 0 0 0 0 1 0 28.5714
0
0 0 0 0 0 0 0 1 32.1429 |
En la manivela de la figura, calcular el
par T necesario para transmitir a esa manivela una aceleración
angular
a , calcular también las reacciones en el apoyo C.
Se conoce la carga P, la masa y el momento de Inercia respecto al
centro de gravedad IG . Se supone ya calculada la aceleración
del centro de gravedad aG
Datos:
x = 0.025 m y = 0.035 m
u = 0.015 m v = 0.020 m
m = 0.2 kg Ig = 0.1 kgm2
aGx = 0.1 m/s2 aGy
= 0.1 m/s2
Px = 1 N Py = 1 N
a= 2 rad/s2
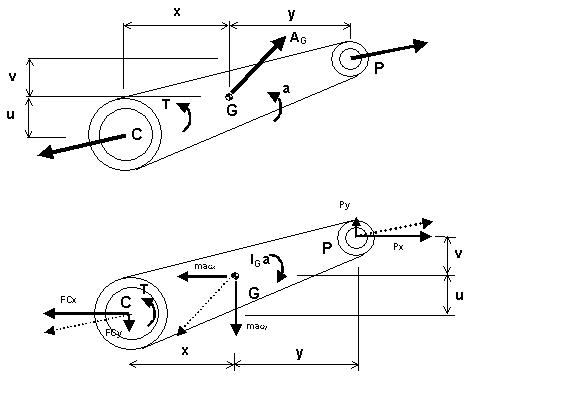
Fcx = Px – maGx
Fcy = Py - maGy
T + Fcy.x – Fcx.u = Px.v – Py.y + Ig.a
Resolver el sistema anterior
Descomposición
LU
Se descompone la matriz A como producto
de dos matrices triangulares A=LU ( L, matriz triangular inferior y U,
triangular superior). Si el sistema original es AX=C, se tiene L(UX)=C.
Se resuelve LY=C y una vez hallado Y se resuelve el sistema UX=Y, de forma
que se obtiene la solución buscada.
El método para realizar la descomposición
consiste en aplicar el método de Gauss sin permutar las filas.
La función [L,U]=lu(A), nos devuelve
L y U.
Nota: siempre se puede aplicar la factorización
LU.
Ejemplo:
EDU»
A=[1 3;7 9];
EDU»
[L,U]=lu(A)
L
=
0.1429
1.0000
1.0000
0
U
=
7.0000
9.0000
0
1.7143
EDU»
L*U % conprobación
ans
=
1
3
7
9 |
|